经济利润问题在考试中经常会出现,对于考试中经济利润问题会涉及到基本公式类,分段计费类,和费用统筹类。而让我们利益最大化实际就是费用统筹类,费用统筹类在考试过程中我们通常会碰到最优方案和最大利润两类。接下来就费用统筹类做讲解。
一、最优方案类
最优方案在生活中经常也会碰到,就像在商场做活动,存在多种不同的活动形式,这时候我们要选择哪个活动才会让我们花的钱最少呢?
题目特征:多个方案选择,花的钱最少
方法:花最少的钱而获得最多的东西。对于这类题我们做题的时候分情况、分方案进行讨论,找到成本最低的一个方案就好。
【例1】某商场会员全年购买该商场商品可享8折优惠,近日该商场举行店庆优惠活动。全场商品满199元减50元,满399元减100元,满599元减200元,会员优惠和店庆优惠每次只能享受一项。活动期间会员小兴分三次购买了价值260元、480元、640元商品各一件,则小兴最少需支付:
A. 1024元
B. 1026元
C. 1028元
D. 1030元
【解析】第一步,对于本题要求最少支付的钱数,题干中存在两种不同的活动形式,对于这种题目属于费用统筹类的选择最优方案。
第二步,对于选择最优方案类,分情况进行讨论。
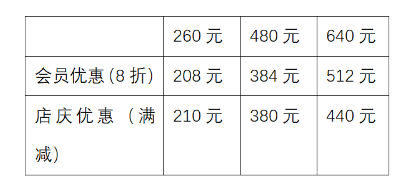
对于三件商品分别进行选择最优的方案,因此,260元的商品选择参加会员优惠,480元的商品选择参加店庆活动,640元的商品选择参加店庆活动。
所以,小兴最少需要支付208+380+440=1028(元)。
因此,选择C选项。
【例2】某镇政府有工作人员104人,他们在清明节前去烈士陵园缅怀革命先烈,需全部坐船渡过一条河。已知大船可载客12人,小船可载客5人,大船和小船不论坐满与否,都按满载算。若大船渡一次70元,小船渡一次30元,则他们渡河最节省的方案是:
A. 7只大船和4只小船
B. 2只大船和16只小船
C. 6只大船和2只小船
D. 1只大船和20只小船
【解析】第一步,本题要选出最节省的方案,即选择最优方案,选项给出不同的方案,可以用代入排除法。
第二步,大船可载12人,小船可载5人,共104人,代入A选项,7只大船4只小船可载7×12+4×5=104(人),共需费用70×7+30×4=610(元);代入B选项,2只大船16只小船可载2×12+16×5=104(人),共需费用70×2+30×16=620(元);代入C选项,6只大船2只小船可载6×12+2×5=82<104(人),直接排除;代入D选项,1只大船20只小船可载1×12+20×5=112>104(人),共需费用70×1+30×20=670(元)。对比可得A选项可载全部104人且花费最少。
因此,选择A选项。
二、最大利润类
题目特征:单价和销量此消彼长,问何时总价或总利润最高?
方法:设提价次数为 x。
(1)令总价或总利润为 0,解得![]() 、;
、;
(2)当时![]() ,取得最值。
,取得最值。
【例】某商品的进货单价为80元,销售单价为100元,每天可售出120件,已知销售单价每降低1元,每天可多售出20件。若要实现该商品的销售利润最大化,则销售单价应降低的金额是:
A.5元
B.6元
C.7元
D.8元
【解析】第一步,本题涉及单价降低,销量增加的过程,属于费用统筹的最大利润类。
第二步,设降价x元,即降了x个1元,可得![]() ,令销售总利润为0,解得
,令销售总利润为0,解得![]() 。当
。当 时,销售总利润取得最值,也就是要实现该商品的销售利润最大化,则销售单价应降价7元。
时,销售总利润取得最值,也就是要实现该商品的销售利润最大化,则销售单价应降价7元。
因此,选择C选项。


 |
| 
 国考系列课程
国考系列课程











