2024年山东选调生考试行测备考:数量关系之最值问题应该这样备考
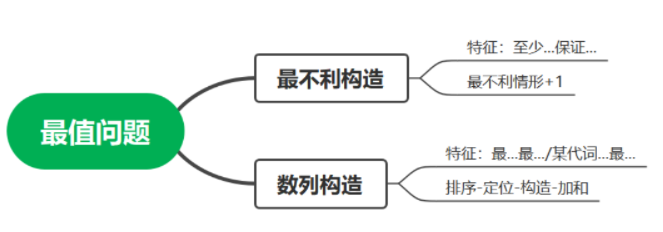
数量关系最值问题是公务员考试里面常考的题型之一,但是难度没有那么大,常见的最值问题包括两大题型,分别是最不利构造和数列构造。
题型一:看我如何搞定最不利构造
例1:某演唱会主办方为观众准备了白红橙黄绿蓝紫7种颜色的荧光棒各若干只,每名观众可在入口处任意选取2只,若每种颜色的荧光棒都足够多,那么至少( )名观众中,一定有两人选取的荧光棒颜色完全相同。
A.14
B.22
C.28
D.29
【答案】D
【解析】第一步,本题考查最不利构造。

例2:某会展中心布置会场,从花卉市场购买郁金香、月季花、牡丹花三种花卉各20盆,每盆均用纸箱打包好装车运送至会展中心,再由工人搬运至布展区。问至少要搬出多少盆花卉才能保证搬出的鲜花中一定有郁金香?
A. 20盆
B. 21盆
C. 40盆
D. 41盆
【答案】D
【解析】第一步,本题考查最值问题,属于最不利构造。 第二步,根据“至少……保证……”可知本题为最不利构造,答案为“所有最不利情况+1”。要求搬出的鲜花中一定有郁金香,最不利的情况是把所有月季花、牡丹花都搬出来,即搬出20+20=40(盆)。在此基础上再搬1盆,就能够保证搬出的鲜花中一定有郁金香,即至少要搬出40+1=41(盆)。 因此,选择D选项。
题型二:数列构造掌握规律也不难噢!
例1:从某物流园区开出6辆货车,这6辆货车的平均装货量为62吨,已知每辆货车载重量各不相同且均为整数,最重的装载了71吨,最轻的装载了54吨。问这6辆货车中装货第三重的卡车至少装载了多少吨?
A. 59
B. 60
C. 61
D. 62
【答案】B
【解析】第一步,本题考查最值问题,属于数列构造。 第二步,总和一定,求某项最值,使用数列构造的方法。首先,根据题意将6辆货车的载重量从大到小排序则第一重的为71吨,最轻的为54吨,求第三重的卡车至少载重多少,则其余货车载重尽量多,设第三重的卡车至少载重x吨,那么构造排名第二至第五的载重依次为:70,x,x-1,x-2。可列方程:71+70+x+(x-1)+(x-2)+54=62×6,解得x=60。 因此,选择B选项。
例2:某高校计划招聘81名博士,拟分配到13个不同的院系,假定院系A分得的博士人数比其他院系都多,那么院系A分得的博士人数至少有多少名?
A. 6
B. 7
C. 8
D. 9
【答案】C
【解析】第一步,本题考查最值问题中的数列构造问题。 第二步,总共招聘81名博士,要想院系A分得的博士数最少,则应构造其余院系分得的博士数尽可能多。设院系A分得博士x名,那么其余12个院系最多均有x-1名,可列方程:x+(x-1)×12=81,解得x≈7.2,那么院系A分得的博士至少有8名。 因此,选择C选项。