数量关系备考技巧：如何突破排列组合问题

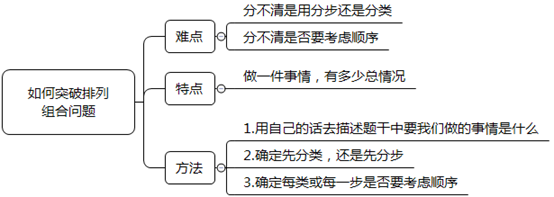
　　在数学运算中，排列组合是一种必考题型，但确是很多同学难以跨过的坎。题目做的越多越困惑，有的时候是用加法，有的时候又是用乘法;有的时候要考虑顺序，有的时候不用考虑顺序，甚至还要在列出的式子上去掉顺序;当然最坏的情况是面对一个排列组合的题根本就不知道从何入手。如果大家存在着这些问题，有必要耐住性子好好看看这篇文章，可以帮助你在面对排列组合问题时快速找到突破口，列出正确的式子，选出正确的选项。

　　排列组合的题目一般都是要我们去做一件事情，然后问做这件事有多少种完成情况。大家可以思考一下我们在决定做一件事情时，是不是会先对一件事情进行分解，把复杂的问题简单化，我们在进行分解时一般会从两个角度进行思考，一个是要不要分情况讨论，另一个是要不要分成多个步骤。当然我们思考问题的角度不一样，列出的式子肯定也不相同，但只要我们的思考的角度能把事情完整的解决掉，最终的答案肯定是一样的，只是从不同角度考虑难易程度不一样。所以在平时练习的时候可以多角度的去思考，去相互印证。

　　在这里我建议大家平时在练习排列组合问题时，可以分三个步骤去进行(不要怕麻烦)。第一步，用自己的话去描述题干中要我们做的事情是什么。第二步，根据题干的限制条件思考做这件事情要先分情况去讨论，还是直接分成多个步骤去完成。第三步，在每一种情况下或每一个步骤下分清楚用A还是C去表示。

　　光说不练假把式，接下来给大家分析几个例题。

　　【例1】某班共有8名战士，现在从中挑出4人平均分成两个战斗小组分别参加射击和格斗考核，问共有多少种不同的方案?

　　A.210

　　B.420

　　C.630

　　D.840

　　【例2】小王等6名学生参与了某展览会志愿者活动。他们被安排到两个不同的会场服务。如果要求每个会场都至少有2名志愿者，则对小王等人共有_______种不同的安排方式。

　　A.20

　　B.30

　　C.50

　　D.360

　　三步走分析下这个题。第一步，这个题要我们做的事情是把6个人分成两个不同的组，且每组人数不得少于2个人。第二步，做这个事情可以分三种情况来讨论。第三步，每个会场内的人数不需要考虑内部的顺序。具体如下表所示：

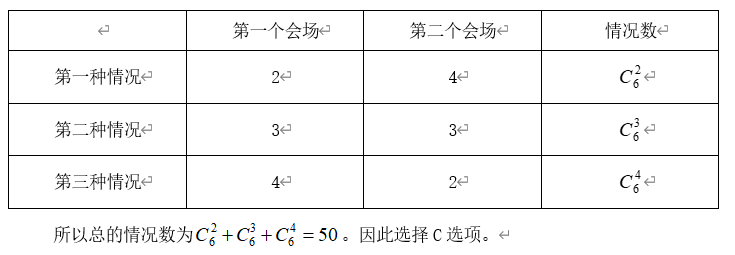
　　所以总的情况数为。因此选择C选项。